fit¶

Note

Functions for fitting 2D data.

Module author: Adam Gagorik <adam.gagorik@gmail.com>

class fit.Fit(x, y, func, popt=None, yerr=None)[source]¶

Base class for fitting.

Parameters:	x (list) – array of x-values y (list) – array of y-values func (function) – function object popt (list) – initial guess for parameters

Warning

Do not explicitly create Fit instance, its a base class.

>>> fit = FitLinear([1, 2, 3], [4, 5, 6])

plot(xmin=None, xmax=None, xpoints=100, **kwargs)[source]¶

Wrapper around matplotlib.pyplot.plot(). Plots the fit line.

Parameters:	xmin (float) – min x-value xmax (float) – max x-value xpoints (int) – number of xpoints

>>> fit = FitLinear([1, 2, 3], [4, 5, 6])
>>> fit.plot(xmin=-1.0, xmax=1.0, xpoints=10, lw=2, color='blue')

text(s, x, y=None, transform=None, rotate=False, draw_behind=True, **kwargs)[source]¶

Wrapper around matplotlib.pyplot.text(). Useful for putting text along the fit line drawn by Fit.plot(), and rotating the text using the derivative.

Parameters:	s (str) – text x (float) – x-value of text y (float) – y-value of text; if None, use the fit line transform (`matplotlib.transforms.Transform`) – matplotlib transform; if None, plt.gca().transAxes rotate (bool) – rotate text using angle computed from derivative draw_behind (bool) – hide the plot objects behind the text

>>> fit = FitLinear([1, 2, 3], [4, 5, 6])
>>> fit.text('Hello!', 0.1, rotate=True, fontsize='large')

solve(y=0, x0=0, return_y=False, **kwargs)[source]¶

Wrapper around scipy.optimize.fsolve(). Solves y=fit(x) for x.

Parameters:	y (float) – y-value x0 (float) – initial guess return_y (bool) – return x and fit(x)
Returns:	xval, yval

>>> fit = FitLinear([1, 2, 3], [4, 5, 6])
>>> xval, yval = fit.solve(y=0, x0=1.0)

brute(a=0, b=1, find_max=False, return_y=False, **kwargs)[source]¶

Wrapper around scipy.optimize.brute(). Finds minimum in range.

Parameters:	a (float) – lower x-bound b (float) – upper x-bound find_max (bool) – find max instead of min return_y (bool) – return x and fit(x)
Returns:	xval, yval

>>> fit = FitLinear([1, 2, 3], [4, 5, 6])
>>> xval, yval = fit.brute(a=-1, b=1)

maxbrute(a=0, b=1, return_y=False, **kwargs)[source]¶: Calls Fit.brute() with find_max=True

minimize(x0=0, find_max=False, return_y=True, **kwargs)[source]¶

Wrapper around scipy.optimize.minimize(). Finds minimum using a initial guess.

Parameters:	x0 (float) – initial guess for x find_max (bool) – find max instead of min return_y (bool) – return x and fit(x)
Returns:	xval, yval

>>> fit = FitLinear([1, 2, 3], [4, 5, 6])
>>> xval, yval = fit.minimize(x0=0.1)

maximize(x0, return_y=True, **kwargs)[source]¶: Calls Fit.minimize() with find_max=True

derivative(x, **kwargs)[source]¶

Wrapper around scipy.misc.derivative(), unless an inheriting class implements the derivative analytically.

Parameters:	x (float) – x-value to evaluate derivative at
Returns:	float

tangent(x, **kwargs)[source]¶

Compute a tangent line at x.

Parameters:	x (float) – x-value to evaluate derivative at xmin (float) – min x-value xmax (float) – max x-value xpoints (int) – number of xpoints

>>> fit = FitLinear([1, 2, 3], [4, 5, 6])
>>> func = fit.tangent(x=1.5)
>>> print func(1.5)
... 0.0

plot_tangent(x, xmin=None, xmax=None, xpoints=100, **kwargs)[source]¶

Plot a tangent line at x.

Parameters:	x (float) – x-value to evaluate derivative at xmin (float) – min x-value xmax (float) – max x-value xpoints (int) – number of xpoints

>>> fit = FitLinear([1, 2, 3], [4, 5, 6])
>>> fit.plot_tangent(x=1.5, lw=2, color='blue')

summary()[source]¶

Create a summary dict of fit results.

Returns:	`dict`

sort(**kwargs)[source]¶: Sort x and y values.

class fit.FitPower(x, y, order=1, popt=None, yerr=None)[source]¶

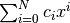
$\sum_{i=0}^{N} c_i x^i$

Parameters:	order (int) – order of polynomial

summary()[source]¶: create a summary dict

class fit.FitLinear(x, y, popt=None, yerr=None)[source]¶

$m x + b$

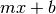
derivative(x, **kwargs)[source]¶: analytic derivative of function

summary()[source]¶: create a summary dict

class fit.FitQuadratic(x, y, popt=None, yerr=None)[source]¶

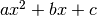
$a x^{2} + b x + c$

derivative(x, **kwargs)[source]¶: analytic derivative of function

summary()[source]¶: create a summary dict

class fit.FitInterp1D(x, y, popt=None, yerr=None, **kwargs)[source]¶

Fit to interpolating function.

Parameters:	kind (str) – linear, nearest, zero, slinear, quadratic, cubic.

kind : linear, nearest, zero, slinear, quadratic, cubic

class fit.FitUnivariateSpline(x, y, popt=None, yerr=None, **kwargs)[source]¶

Fit to spline.

Parameters:	k – degree of spline (<=5)

class fit.FitLagrange(x, y, popt=None, yerr=None)[source]¶: Fit to lagrange interpolating spline. It sucks.

class fit.FitBarycentric(x, y, popt=None, yerr=None, **kwargs)[source]¶: Fit to lagrange interpolating spline. It sucks.

class fit.FitTanh(x, y, popt=None, yerr=None)[source]¶

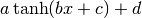
$a \tanh(b x + c) + d$

derivative(x, **kwargs)[source]¶: analytic derivative of function

summary()[source]¶: create a summary dict

class fit.FitLog(x, y, popt=None, yerr=None)[source]¶

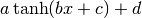
$a \tanh(b x + c) + d$

derivative(x, **kwargs)[source]¶: analytic derivative of function

summary()[source]¶: create a summary dict

class fit.FitXTanh(x, y, popt=None, yerr=None)[source]¶

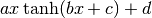
$a x \tanh(b x + c) + d$

derivative(x, **kwargs)[source]¶: analytic derivative of function

summary()[source]¶: create a summary dict

class fit.FitErf(x, y, popt=None, yerr=None)[source]¶

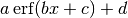
$a\,\mathrm{erf}(b x + c) + d$

summary()[source]¶: create a summary dict

class fit.FitXErf(x, y, popt=None, yerr=None)[source]¶

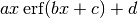
$a x\,\mathrm{erf}(b x + c) + d$

summary()[source]¶: create a summary dict

class fit.FitGaussian(x, y, popt=None, yerr=None)[source]¶

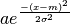
$a e^{\frac{-(x - m)^{2}}{2 \sigma^{2}}}$

summary()[source]¶: create a summary dict

class fit.FitSin(x, y, popt=None, yerr=None)[source]¶

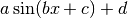
$a \sin(b x + c) + d$

derivative(x, **kwargs)[source]¶: analytic derivative of function

summary()[source]¶: create a summary dict

class fit.FitCos(x, y, popt=None, yerr=None)[source]¶

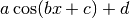
$a \cos(b x + c) + d$

derivative(x, **kwargs)[source]¶: analytic derivative of function

summary()[source]¶: create a summary dict

class fit.FitLinearZero(x, y, popt=None, yerr=None)[source]¶

$mx$

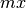
derivative(x, **kwargs)[source]¶: analytic derivative of function

summary()[source]¶: create a summary dict

class fit.FitQuadraticZero(x, y, popt=None, yerr=None)[source]¶

$mx$

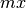
derivative(x, **kwargs)[source]¶: analytic derivative of function

summary()[source]¶: create a summary dict

Previous topic

Next topic

This Page

fit¶

Navigation

Previous topic

Next topic

This Page

Quick search

fit¶

Navigation